Wisteria - Lexer
The typical approach used to construct a lexer as described in the “Dragon Book”, is to convert a regular expression to a non-deterministic finite automaton (NFA), and then to convert this automaton into a deterministic automaton (DFA). This latter step is a fairly expensive process where the \(\epsilon\)-closure of each of the NFA’s states must be calculated. That is, for all of the states in an NFA, we must find all the other states that are reachable by an \(\epsilon\)-transition.
Wisteria’s lexer generator follows the descriptions given by Owen, et al. in Regular-expressions derivative reexamined. As they conclude in this paper, their approach provides a way to directly construct a DFA from the regular expression and the resulting lexers are often optimal and uniformly better that those produced by previous tools. This is done through regular expression derivatives.
Regular Expression Derivatives
The derivative of the language captured by a regular expression with respect to a string \(u\) is the set of strings \(v\) such that \(u\cdot v\) is captured by the regular expression:
\[\partial_u\mathcal L = \{v\mid u\cdot v\in \mathcal L \}\]We can construct the derivative of a regular expression inductively using the following rules:
From Regular-expression derivatives reexamined
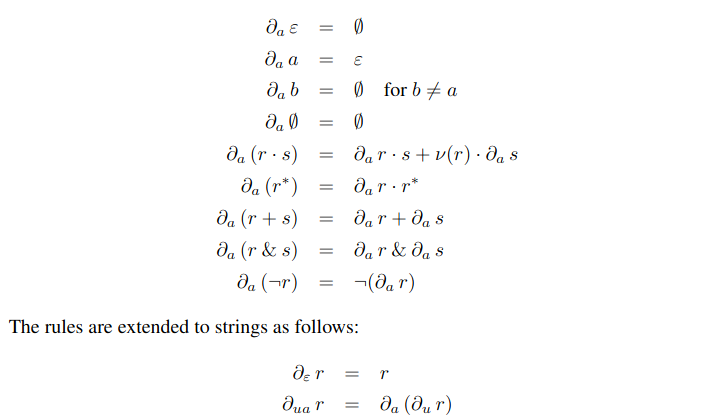
We can now say that a string \(a\cdot u\) matches a regular expression \(r\), if and only if, \(u\) matches \(\partial_a r\). We can thus construct a DFA by precomputing the derivative of the regular expression for each possible symbol in the alphabet (e.g. English, ASCII, Unicode, etc.). The transition function for the resulting DFA is simply the derivative function over the set of equivalent regular expressions. Further details on this algorithm can be found in the paper, including how these derivatives can be found over sets of characters.
Implementing this approach to a lexer generator turned out to be very straightforward. The recursive nature of finding regular expressions led to a very clean implementation, and one that was later easy to debug. Especially when extending into sets of characters, the algebraic methods described in the paper provided an efficient implementation over iterating over all the symbols in the alphabet (an unfeasible task with unicode).
Finally, as a front end to the lexer generator, I designed the Wisl language which defines tokens, their types, and then the corresponding regular expressions that match them.