Delimited Continuations
We should prefer implementing delimited continuations through CPS transformations, rather than piggybacking off existing language constructs such as exception handling. The latter method is not only highly specific to the implementation language, but must also fight with the interactions of the base languages.
In Delimited control in OCaml, abstractly and concretely, Oleg Kiselyov defines and implements an API to implement delimited continuations for languages with exceptions and stack control. However, having a purely native code implementation incurs costs as we shoehorn delimited continuations into a system that was not intended to have them. By applying CPS transforms at compile time, Rompf, Maier, and Odersky in Implementing First-Class Polymorphic Delimited Continuations by a Type-Directed Selective CPS- Transform manage to implement correctly typed delimited continuations in Scala without any runtime overhead.
Delimited continuations in OCaml
The abstract machine that Kiselyov presents in his paper, defines the delimited continuations in terms of stack manipulations. For example, \(\texttt{pushP}\ e\ e'\), Kiselyov’s equivalent to \(\textsf{reset}\), adds a stack frame onto the stack with the current context that can later be retrieved and jumped back to.
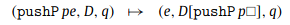
\(\texttt{takeSC}\ p\ v\), the \(\textsf{shift}\) equivalent, then identifies the appropriate stack frame and jumps back to the context it captured, returning an “exception” value.

Two more operations are also defined. \(\texttt{newP}\) creates a new prompt that acts as a handle to anchor the \(\textsf{reset}\) point for a particular continuation. Lastly, \(\texttt{pushSC}\ e\ e'\) allows us to go back to where \(\texttt{takeSC}\) was called to insert a value into where we jumped back from. While this does introduce two extra operations, this is in benefit of allowing multi-prompt continuations which allows us to cross \(\textsf{reset}\) boundaries for different behaviors without conflicting. The next section however, will show how the implementation requires bookkeeping incurring additional costs.
Moreover, by defining the operations in terms of stack manipulations, to implement such a system we must have at our disposal some degree of stack control which most languages lack. Moreover, we abstract away from the standard algebraic semantics, resulting in a much more complicated implementation. Instead of substituting the continuation variable \(k\), for a function that captures the context up to the \(\textsf{reset}\), we delimit, push, identify, copy and retrieve stack frames to implement \(\textsf{reset}\) and \(\textsf{shift}\).
Using exceptions and stack frames
Kiselyov’s OCaml implementation of delimited continuations uses exceptions to accomplish behavior unintended by the language implementers. This means that we must safeguard against the adverse interactions that exceptions have on delimited continuations, while also needing to use the limited stack control operations available. As we will see, both these requirements add an extra overhead.
The operations defined in the previous section are implemented with what Kiselyov dubs the ‘scAPI’, a set of functions that, using exceptions, are able to manipulate the stack. This is achieved by using a dedicated register in the OCaml interpreter that keeps a pointer to the latest exception frame. Oversimplifying for brevity, scAPI is able to delimit stack frames using this exception frame pointer. To then copy and push stack fragments, scAPI leverages OCaml’s stack overflow handling methods that copy the stack onto the heap, where we can manipulate them to implement the delimited continuations. Kiselyov here hides much of the implementation details for the scAPI as we can assume that this involves arcane foreign C code to be able to perform such memory manipulations. Nevertheless, such stack manipulations must introduce a performance overhead as data is copied between separate memory regions.
Kiselyov’s implementation is further complicated when noticing that using multi-prompt continuations means that \(\texttt{takeSC}\) requires locating a particular prompt value on the stack, rather than popping off the topmost frame. Even with OCaml’s stack control mechanisms we cannot search through the stack to identify a particular prompt. This is solved by maintaining a global parallel stack of \(\texttt{pushP}\) invocations that save exception frame pointers and other relevant information. Not only does this incur memory costs, but whenever we unwind the stack when \(\texttt{takeSC}\) is called, we must search through this parallel stack to find the corresponding prompt. This stack manipulation approach thus necessitates this extra bookkeeping even though OCaml’s runtime allows us to retrieve exception frame pointers and copy stack frames. We can imagine extending such a parallel stack to include all the stack’s contents, not just the frame pointers when such mechanisms are not available to us.
It should also be noted that by using exceptions, the implementation must also ensure that any user exceptions and try statements do not interfere with the ones used to implement delimited continuations. This requires every \(\texttt{pushP}\) (i.e. \(\textsf{reset}\)) to further encapsulate a try statement and raise an exception after completing execution. This complicates the program’s control flow, especially when we consider the cost that indirect branches have on modern hardware.
These issues mentioned are not exhaustive as Kiselyov’s implementation further runs into complications when dealing with other aspects of the language. This is all in an effort to keep the implementation as a native OCaml library.
The Scala alternative
Rompf, et al. take a different approach to implementing delimited continuations in Scala. They transform source level Scala code using a type-directed selective CPS transform. Only code that is annotated as being a delimited continuation is therefore transformed, avoiding the grand cost of transforming the entire program. This is done entirely on the stock JVM with Scala’s compiler plugins framework.
In their paper, Rompf, et al. first show how one could perform a syntax-directed selective CPS transform to implement delimited continuations. Importantly, the transform is done selectively, only on relevant code that use their \(\textsf{shift}\) operator. This \(\texttt{Shift}\) operator, implemented as a class of the same name, describes delimited continuations as monads. Mapping functions are provided to apply the surrounding context to each instance of the continuation variable k. \(\textsf{reset}\) is then implemented as a function taking a \(\texttt{Shift}\) object which then invokes its body, passing the result of the computation into it. This essentially directly performs the substitution described in the definition of delimited continuations, a much closer correspondence to the intended semantics than Kiselyov’s implementation:
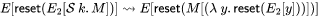
The syntactic transformation is automatically done by Scala’s parser and is perfectly serviceable, but results in a verbose programming style that obfuscates the actual behavior of delimited continuations. To remedy this, Rompf, et al. use Scala’s type annotations to mark any Shift objects that need to be transformed. They define a strict type system of polymorphic continuations, where types are enriched with effects that describe a change of the continuation’s context’s type when the continuation is applied. This type system provides a blueprint for correctly implementing the CPS transforms that limits the need to apply haphazard patches as problems arise – cf. Kiselyov’s implementation.
Rompf, et al.’s transformation rules make use of their type system to ensure that all effects are appropriately captured and chained when dealing with multiple continuations. Whenever a Shift object is used in the source code, we perform the monadic mapping that applies the continuation as described above. So for an expression e of type A and continuation effects B, C, we map all instances of its continuation variable to be invoked in the surrounding context r:
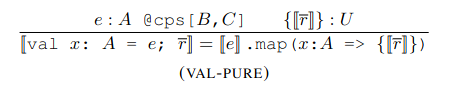
These transformations are implicitly performed at compile time, producing code equivalent to that written by hand using the Shift object. The only overhead comes from potential optimizations that the user could have made in a manual direct implementation. The result is a continuation system that outperformed contemporary continuations systems on the JVM. Moreover, when benchmarked against programs that use lists and streams instead of delimited continuations, Rompf et al’s implementation ran at comparable speeds, while dealing with memory constraints better. In comparison, Kiselyov only compares his implementation with undelimited continuations, which indeed yields better results, but does not serve as a proper frame of reference.
It’s OK to modify the compiler
Kiselyov criticizes Rompf, et al’s implementation “[requiring] modifying the compiler or the run-time, or both.” The argument to be made here is that Kiselyov’s library is compatible with all OCaml code ‘out-of-the-box’. However, this makes it seem as if Rompf, et al. provide a new version of the Scala compiler when in fact they use an API for implementing plugins directly available to the user. Installing such plugins is straightforward and once installed makes continuations compatible with other Scala code. The restriction does remain that without the plugin any libraries with continuations are unusable.
Extending to other programming languages
Kiselyov markets his approach as universal, but only for languages that implement exceptions and expose stack inspection. This greatly limits the languages that can take advantage of his scAPI. Take Rust, which doesn’t support inspection and therefore implementing Kiselyov’s approach in this language would be unfeasible. Rompf, et al.’s implementation on the other hand could very feasibly be implemented directly in Rust using procedural macros. These offer very powerful code transformations that can check for the appropriate typing as defined in the paper. This is further done without having to write a single line of foreign code.
In conclusion, we can liken Kiselyov’s OCaml implementation as using a crowbar to open the front door, whereas Rompf, et al. use the back-door key to get in. The front door is accessible to everyone but using a crowbar naturally has its costs. Instead, using the back-door and modifying the compiler in an intended manner, yields a much better implementation of delimited continuations.